The Blue View - The Great Circle Route

If you were planning a long sea voyage and wanted to take the shortest, most direct route, one way to determine the course would be to take a globe and put a string between the start and end points. Assuming there weren't any landmasses or other obstacles on the route, the string would mark the shortest route.

The string would lie along the great circle joining the two points, which, as defined by Wikipedia, is “a circle on the surface of a sphere that lies in a plane passing through the sphere's center. As it represents the shortest distance between any two points on a sphere, a great circle of the earth is the preferred route taken by a ship or aircraft.”

Few sailors, however, rely on a globe and string for navigation. Instead, routes are planned and plotted using flat paper charts (or, more likely, flat chartplotter screens). A straight line drawn between the start and destination on a traditional Mercator projection chart is called the rhumb line and is not necessarily the shortest route, however. So how is the great circle route determined?

If your math skills are good, the great circle route between any two points on the globe can be calculated using spherical trigonometry. A simpler method is to use another type of chartset, called the Great Circle Sailing Charts. These use a gnomonic projection as opposed to the usual Mercator projection of the world. On a gnomonic projection, the lines of latitude are drawn as arcs. A straight line drawn between any two points on these charts lies along the great circle between the points, and is the shortest possible route. The great circle charts cannot be used for navigation, however, so the route must be transferred to the usual navigational charts.

Not that many years ago, to create a great circle route, I would plot the route on the gnomonic charts. Then I would create and measure waypoints along the great circle route a few hundred miles apart, and transfer them to the Mercator charts. If I connected the dots, I would then have a close approximation to the great circle route on our regular paper charts. The route would then have to be closely checked to make sure we weren't going to sail through a reef or island. It took a lot of time and it was quite easy to make errors, so Marcie would always check my work.

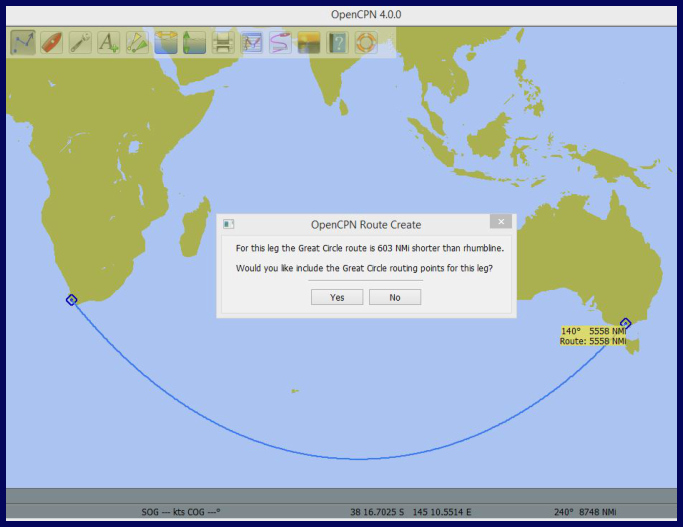
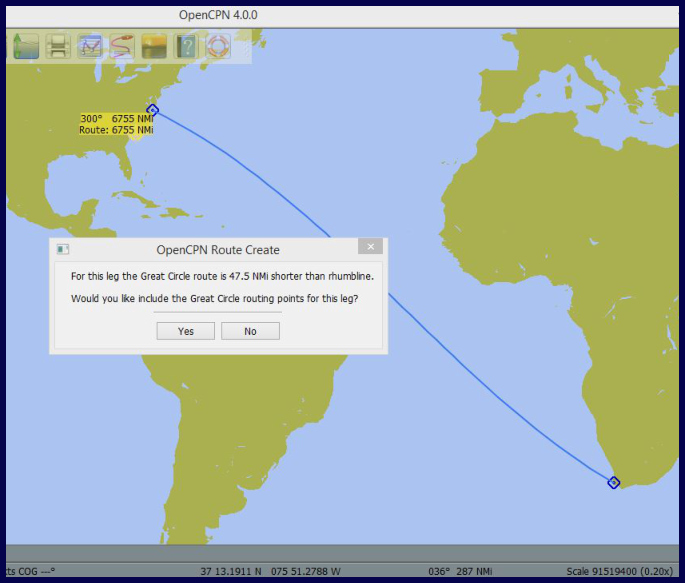
Now, of course, chartplotters do all the work for us. For example, when plotting a course on OpenCPN, a PC-based navigation program that we use, when the correct options are set, the program will display the difference in nautical miles between the rhumb line route and the great circle route and will then plot the route either way. A nice feature!

Some rules of thumb regarding great circle routes:

Since lines of longitude are great circles of the earth, the rhumb line for a route that runs north-south will also be a great circle route. The only latitude line that is also a great circle is the equator. The further an east-west route is from the equator, the more the rhumb line distance will vary from the great circle distance. For example, if sailing from Cape Town to Melbourne, the rhumb line is more than 600 nm longer than the great circle route, while the difference between the rhumb line and great circle distances for a route between Ecuador and New Guinea is only about 85 nm.

On long passages that run both east-west and north-south, the difference between the rhumb line and great circle distances is often very small. An example is the route from Cape Town to New York, which varies only about 50 nm between the rhumb line and the great circle distances.